# JavaScript 中常见的排序类型
# 前言
此文浅总结了常见的几大排序,并介绍了相关特性和优化方式。对稳定性、复杂度的含义和分析也做了简单说明,另外对于递归函数中,分析时间复杂度的master公式也做了阐述,希望对你有用。
# 排序
# 冒泡排序
冒泡排序(Bubble Sort)非常形象,数组在每次循环时,从左至右,相邻元素两两比较,将最大的元素逐渐交换到最后,每一轮循环最大元素在视觉上像是冒泡一样上浮到数组末尾。
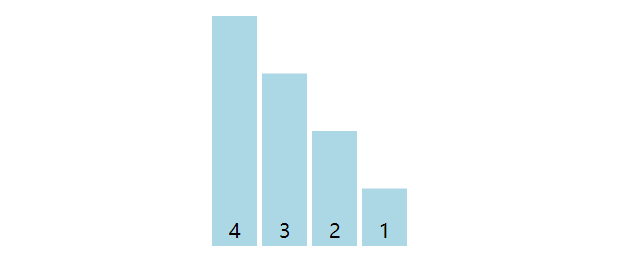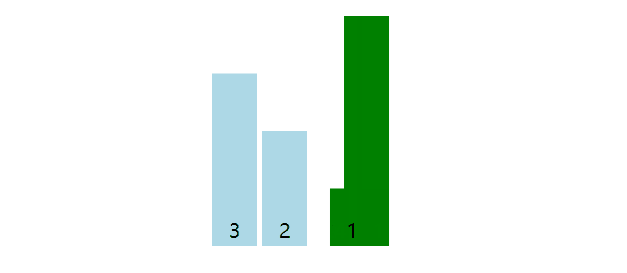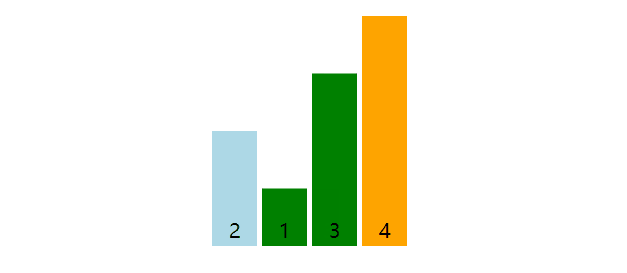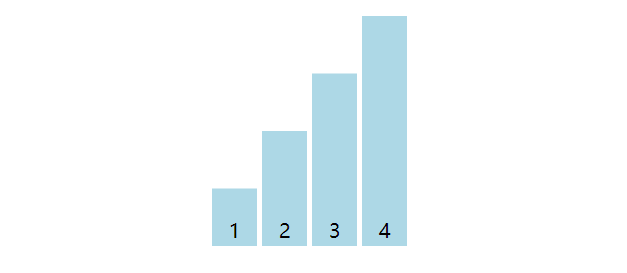
以数组[4, 3, 2, 1]为例子,数组前一个元素与后一个元素比较,若前一个元素大则交换,一轮下来最大值被交换至末尾。数量上共计3(4 - 1)轮,第一轮将4放在末尾,第二轮将3放在末尾,第三轮将2放在末尾。
for (var i = 0; i < 3; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1)
}
}
// [3, 2, 1, 4]
for (var i = 0; i < 2; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1)
}
}
// [2, 1, 3, 4]
for (var i = 0; i < 1; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1)
}
}
// [1, 2, 3, 4]
;swap用于交换数组两个元素。
function swap(arr, i, j) {
var temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
// ES6
function swap(arr, i, j) {
;[arr[i], arr[j]] = [arr[j], arr[i]]
}
可以发现,每轮的比较次数都会少一次,原因在于每一轮结束后就会正确排列出一个数,下一轮则不用再比较。例如第一轮结束数组为[3, 2, 1, 4],下一轮时4就不用比较了。
封装为以下函数,其中外层循环用于控制轮数,内层循环用于比较交换。
function bubbleSort(arr) {
for (var i = 0; i < arr.length - 1; i++) {
for (var j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1)
}
}
}
}
# 优化
以数组[1, 2, 3, 4]为例子,第一轮所有元素都没有发生交换,说明数组的顺序已经达到要求,可以跳出不用继续循环了。
function bubbleSort(arr) {
for (var i = 0, isChange; i < arr.length - 1; i++) {
isChange = false
for (var j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1)
isChange = true
}
}
if (!isChange) return
}
}
# 特性
最优情况下,数组已经是升序,例如[1, 2, 3, 4],比较次数为3次。对于长度为n的升序数组,比较次数则为n - 1,所以时间复杂度为O(n)。
最坏情况下,数组是降序,例如[4, 3, 2, 1],比较次数为3 + 2 + 1 = 6次。对于长度为n的降序数组,比较次数则为(n - 1) + (n - 2) + ... + 2 + 1,即n * (n - 1) / 2次,所以时间复杂度为O(n2)。
一般讨论的时间复杂度均是最坏情况下的时间复杂度,保证算法的运行时长不会比最差情况更长,因此冒泡排序的时间复杂度为O(n2)。另外冒泡排序的空间复杂度为常数级,即O(1)。
冒泡排序也属于原地排序,即未占用额外空间,并且在原数组上发生的交换。
冒泡排序也属于稳定排序。
何为稳定性呢?即排序后相同值元素的原始顺序不改变。
举个例子,若数组为[3, 2, 3', 1],注意3和3'相等都是数值3,此处用于区分两者说明问题。冒泡排序结束后,数组为[1, 2, 3, 3']。排序前3位于3'前面,排序后3同样也是位于3'前面,此特性就是稳定性。
# 选择排序
选择排序(Selection Sort)也非常形象,实际上是在冒泡排序思路上的进一步优化。思考一下,冒泡排序过程中,为了将最大元素冒泡到数组末尾,两两元素交换是否有必要。结果当然是不必要,每一轮比较过程中,仅记录最大元素的索引值即可,一轮在结束时再去将最大元素交换到末尾即可。每一轮循环在视觉上相当于选择出最大元素,然后交换至末尾。
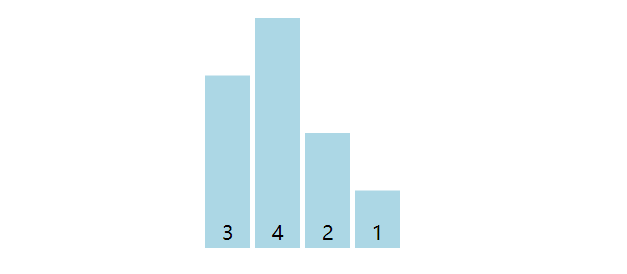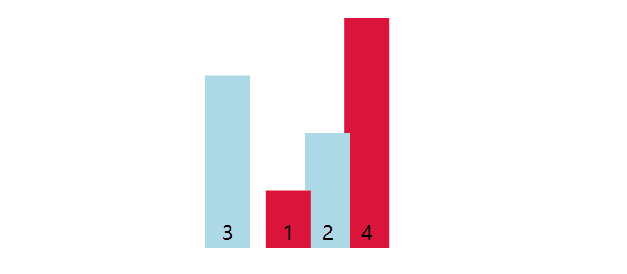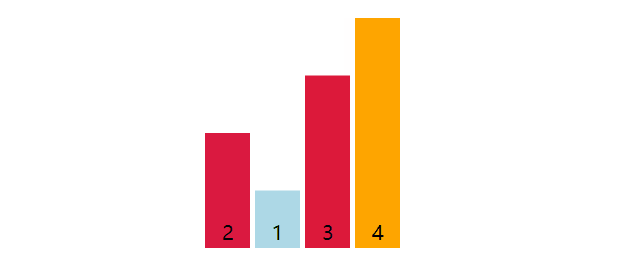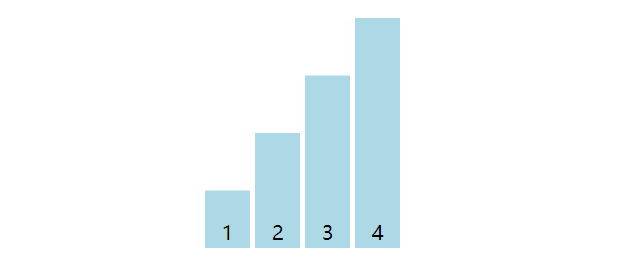
以数组[3, 4, 2, 1]为例子,默认最大元素索引值为0,数组从索引1元素开始遍历,当元素值大于最大元素,则最大元素索引值更新为当前索引值。共计3(4 - 1)轮,第一轮选择出4,第二轮选择出3,第三轮选择出2。
var maxIndex = 0
for (var i = 1; i < 4; i++) {
if (arr[i] > arr[maxIndex]) {
maxIndex = i
}
}
swap(arr, maxIndex, 3)
// [3, 1, 2, 4]
var maxIndex = 0
for (var i = 1; i < 3; i++) {
if (arr[i] > arr[maxIndex]) {
maxIndex = i
}
}
swap(arr, maxIndex, 2)
// [2, 1, 3, 4]
var maxIndex = 0
for (var i = 1; i < 2; i++) {
if (arr[i] > arr[maxIndex]) {
maxIndex = i
}
}
swap(arr, maxIndex, 1)
// [1, 2, 3, 4]
也能发现,每轮比较次数都会少一次,原因也是每一轮都会正确排列出一个元素,下一轮不用再比较。另外每一轮循环结束,还要将最大元素交换至末尾。
封装为以下函数,外层循环控制轮数,内存循环用于比较更新最大索引。
function selectionSort(arr) {
for (var i = 0, maxIndex; i < arr.length - 1; i++) {
maxIndex = 0
for (var j = 1; j < arr.length - i; j++) {
if (arr[j] > arr[maxIndex]) {
maxIndex = j
}
}
swap(arr, maxIndex, j - 1)
}
}
# 特性
选择排序的时间复杂度为O(n2),虽然与冒泡排序的时间复杂度一致,但是元素的交换次数很少,最多交换n - 1次,而冒泡排序则远不止,因此性能上选择排序优于冒泡排序。空间复杂度上选择排序为O(1)。
选择排序也属于原地排序,但是选择排序不稳定。
为什么呢?
还是以[3, 2, 3', 1]数组为例子,第一轮开始maxIndex为0,遍历过程中maxIndex未发生改变,结束时数组为[1, 2, 3', 3]。明显发现,排序前3位于3'前面,排序后3却位于3'后面,因此选择排序是不稳定的。
# 插入排序
插入排序(Insertion Sort)也非常形象,思路上相对复杂一点,但是也很好理解。取出数组的一个元素,依次与前面元素比较,若前面元素较大,则将前面元素后移,否则插入放回。视觉上确实是将元素值插入到数组前面。
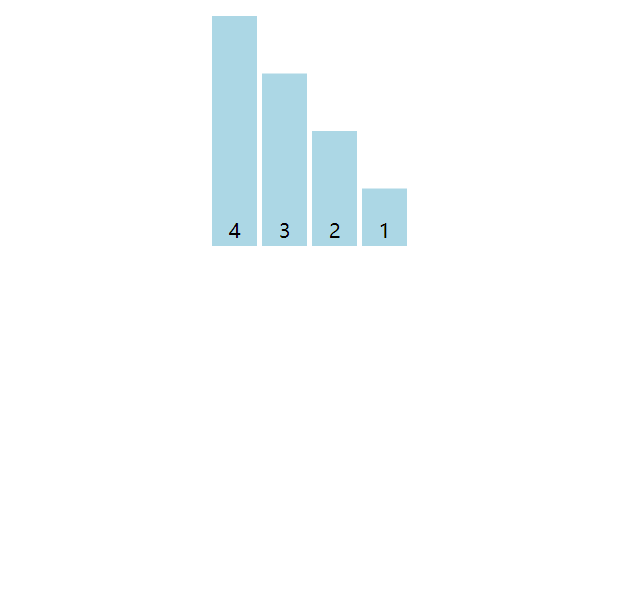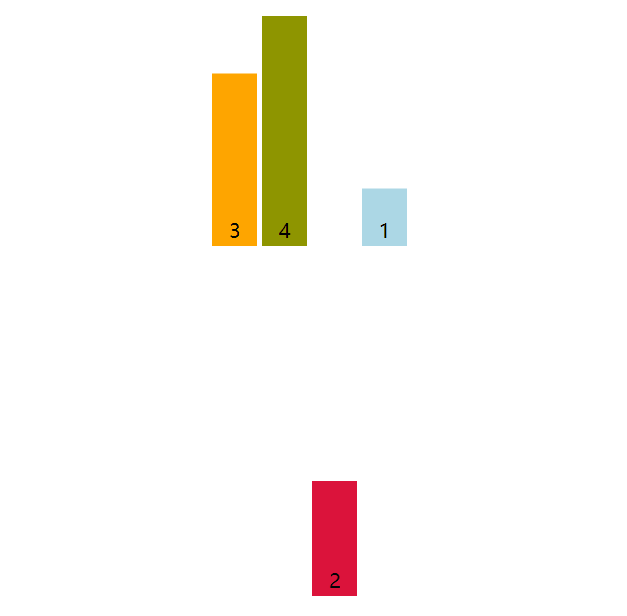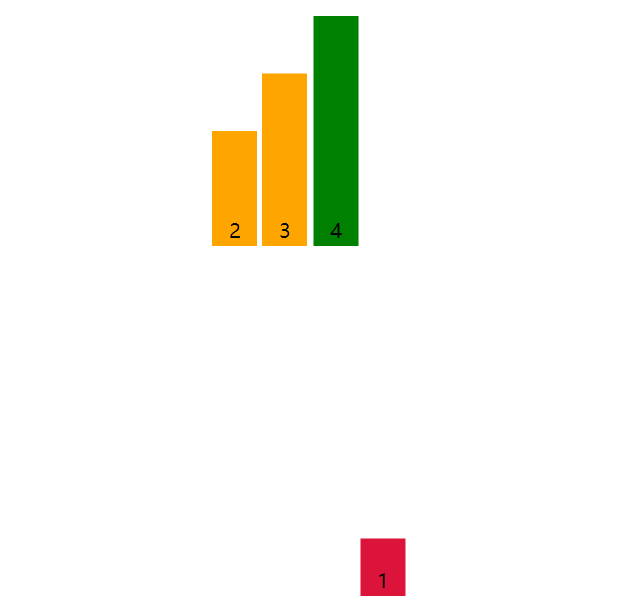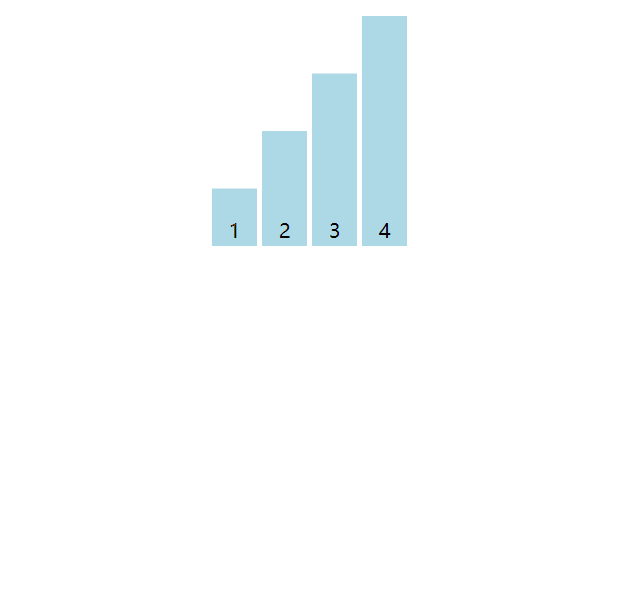
以数组[4, 3, 2, 1]为例子,取出元素3,与前面的元素依次比较,4大于3,将4后移动一位至索引1位置,而3则插入到索引0处。共计3轮,第一轮插入3,第二轮插入2,第三轮插入1。
var current = arr[1]
var i = 0
while (i > -1 && arr[i] > current) {
arr[i + 1] = arr[i]
i--
}
arr[i + 1] = current
// [3, 4, 2, 1]
var current = arr[2]
var i = 1
while (i > -1 && arr[i] > current) {
arr[i + 1] = arr[i]
i--
}
arr[i + 1] = current
// [2, 3, 4, 1]
var current = arr[3]
var i = 2
while (i > -1 && arr[i] > current) {
arr[i + 1] = arr[i]
i--
}
arr[i + 1] = current
// [1, 2, 3, 4]
封装为以下函数,其中外层循环控制轮数并取出元素,内层循环用于比较并右移元素。
function insertionSort(arr) {
for (var j, current, i = 1; i < arr.length; i++) {
current = arr[i]
j = i - 1
while (j > -1 && arr[j] > current) {
arr[j + 1] = arr[j]
j--
}
arr[j + 1] = current
}
}
# 特性
最优情况下,数组已经是升序,例如[1, 2, 3, 4],比较次数为3次。对于长度为n的升序数组,比较次数为n - 1,所以时间复杂度为O(n)。
最坏情况下,数组是降序,例如[4, 3, 2, 1],比较次数为1 + 2 + 3 = 6次。对于长度为n的降序数组,比较次数则为1 + 2 + ... + (n - 2) + (n - 1),即n * (n - 1) / 2次,所以时间复杂度为O(n2)。另外插入排序的空间复杂度为常数级O(1)。
插入排序也属于原地排序和稳定排序。
# 归并排序
归并排序(Merge Sort)即递归与合并,是分而治之思想的典型例子,先递归将原数组二分拆为多个单数组,然后以合并两个有序数组为核心,持续合并为有序数组。
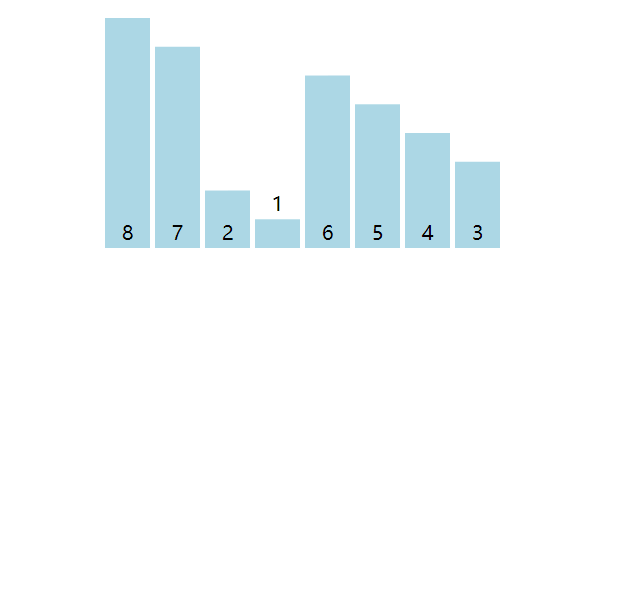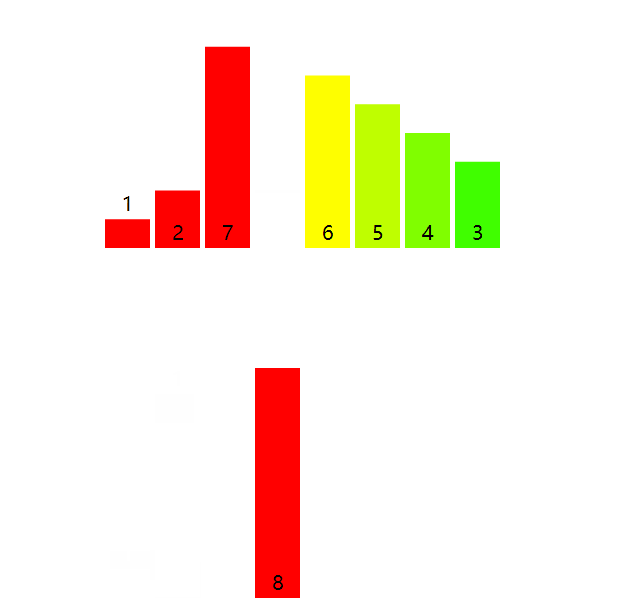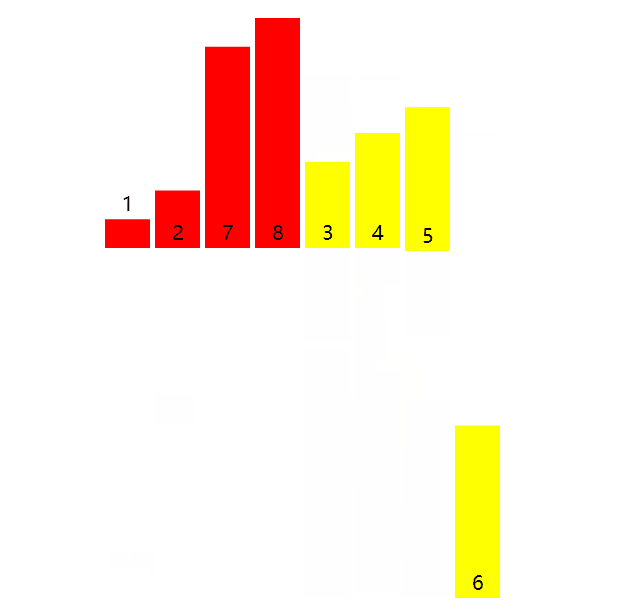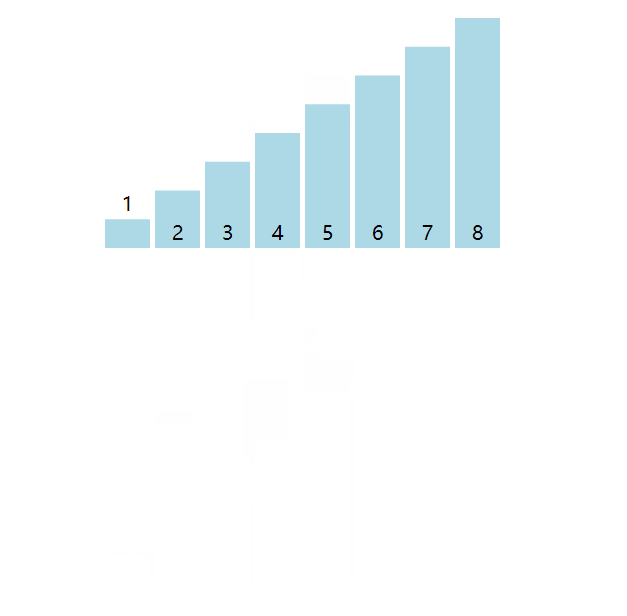
以数组[8, 7, 2, 1, 6, 5, 4, 3]为例子,将数组从中部持续拆分下去,拆分为8个单数组(例如[8]或[7]等等)结束,单数组必然是有序的。然后考虑两个有序数组合并的问题,并持续合并成有序的数组。
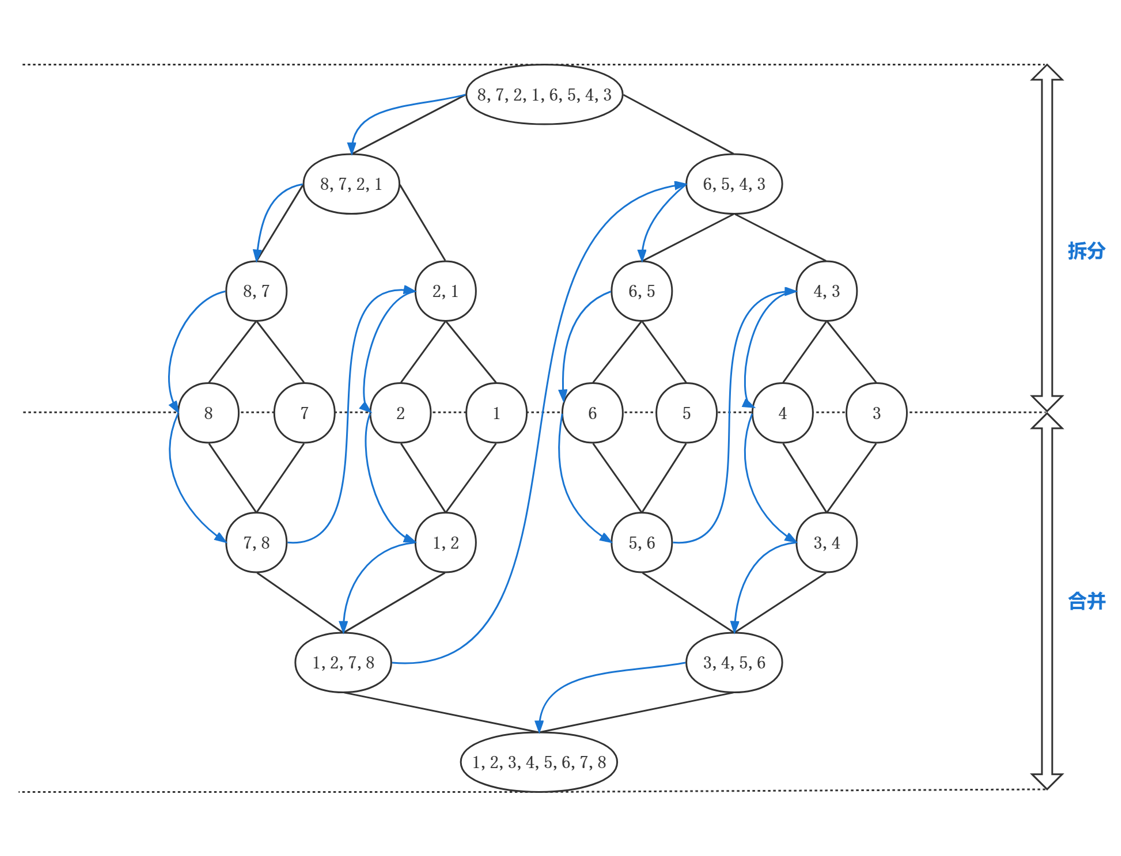
封装为以下函数,其中mergeSort用于递归拆分数组为单数组,merge用于合并两个有序的数组。
function mergeSort(arr) {
var len = arr.length
if (len < 2) return arr
var middleIndex = Math.floor(len / 2)
var left = arr.slice(0, middleIndex)
var right = arr.slice(middleIndex)
return merge(mergeSort(left), mergeSort(right))
}
function merge(left, right) {
var result = []
while (left.length && right.length) {
if (left[0] <= right[0]) {
result.push(left.shift())
} else {
result.push(right.shift())
}
}
if (left.length) {
result.push(...left)
}
if (right.length) {
result.push(...right)
}
return result
}
# master 主定理
递归非常常见,编写出的代码也相当简洁。但是相对于循环程序,递归的时间复杂度却难以估计,master公式就是用于估计递归程序的时间复杂度的。
以下为各变量的含义,注意子问题的规模大小要相同。
n:问题的规模大小a:原问题拆分出的子问题个数n / b:每个子问题的规模大小,O(nd):除了递归之外,剩余的程序的时间复杂度
其中常量a、b和d存在三种关系。
logba > d:时间复杂度为O(nlogba)logba = d:时间复杂度为O(ndlogn)logba < d:时间复杂度为O(nd)
提供一个简单的记忆方式,等于关系记为
O(ndlogn)。而大小于关系,logba和d两者谁大,n的指数就是谁
以获取数组最大值为实例,来分析下各种情况的时间复杂度。
function getMax(arr) {
var len = arr.length
if (len < 2) return arr[0]
var middleIndex = Math.floor(len / 2)
var left = arr.slice(0, middleIndex)
var right = arr.slice(middleIndex)
return Math.max(getMax(left), getMax(right))
}
若数组长度为n,执行getMax函数时,会将数组从中间拆分为两个数组。问题即转换为求两个长度为n / 2的数组的最大值。因此数组n求最大值所消耗的时间可以表示为T(n) = T(n / 2) + T(n / 2) + f(n),其中f(n)表示除了递归之外的程序花费的时间,f(n)可以计为O(nd)。
例如getMax中求出左右数组的最大值之后,还要对左右的最大值再求一次最大值,此次花费的时间即为f(n)。
# 大于
;getMax消耗的时间为T(n) = 2T(n / 2) + O(nd),对照master公式明显发现,常数a = 2且b = 2。
除了递归之外,还要额外执行一次Math.max函数,用于求左右最大值的最大值,其时间复杂度为O(1)。很好理解,因为只执行了一次,所以为常数级O(1),故常数d = 0。
现在a = 2,b = 2和d = 0恰好满足logba > d,因此getMax的时间复杂度为O(nlogba) = O(n)。实际上求最大值,一个for循环的时间复杂度也是O(n),故此时递归和循环是一样的。
# 等于
稍微修改下getMax。
function getMax(arr) {
var len = arr.length
if (len < 2) return arr[0]
var middleIndex = Math.floor(len / 2)
var left = arr.slice(0, middleIndex)
var right = arr.slice(middleIndex)
for (var i = 0; i < len; i++) {
...
}
return Math.max(getMax(left), getMax(right))
}
根据刚才的分析,a和b都为2。但是额外增加了一个for循环,f(n)额外时间则为执行for循环和Math.max所花费的时间。很明显for循环的时间复杂度为O(n),因此d = 1。
现在a = 2,b = 2和d = 1恰好满足logba = d,因此getMax的时间复杂度为O(ndlogn) = O(nlogn)。
# 小于
现在来思考一个问题,若getMax函数拆分的数组不是从中间,而是从其它位置呢。比如left为数组的前2 / 3部分,right为数组的后2 / 3部分,虽然说两数组会有重叠部分,但是两数组或者说两子问题的规模是一致的吧,都是2n / 3的规模。
因此getMax消耗的时间为T(n) = 2T(2n / 3) + O(nd),故a = 2,b = 3 / 2。若getMax内部for循环还嵌套了for循环,时间复杂度为O(n2),则d = 2。
现在a = 2,b = 3 / 2和d = 2恰好满足logba < d,因此getMax的时间复杂度为O(nd) = O(n2)。
# 特性
# 时间复杂度
归并排序内部为递归算法,子问题的规模为n / 2且子问题规模一致,master公式为T(n) = 2T(n / 2) + O(nd),因此a = 2,b = 2。除了递归之外,额外的程序即merge合并函数,由于其内部为while循环,merge函数的时间复杂度为O(n),故d = 1。
;a = 2,b = 2,d = 1,符合logba = d条件,时间复杂度为O(ndlogn) = O(nlogn)。
# 空间复杂度
注意归并排序的空间复杂度为O(n),而不是O(nlogn)。
虽然在合并过程中会开辟log2n个长度为n的数组,总占用的空间为nlog2n。但是在排序过程中,始终只有一个merge合并函数执行,而之前的merge函数在执行后会将占用的空间释放。
以长度为8的数组为例,将开辟3(log28)个长度为8的数组,总占用空间为8 * log28 = 8 * 3,merge函数占用的空间长度依次为2, 2, 2, 2, 4, 4, 8。最后一次合并时,merge函数占用的空间才会达到最大长度8,而之前合并占用的空间都已经被释放。
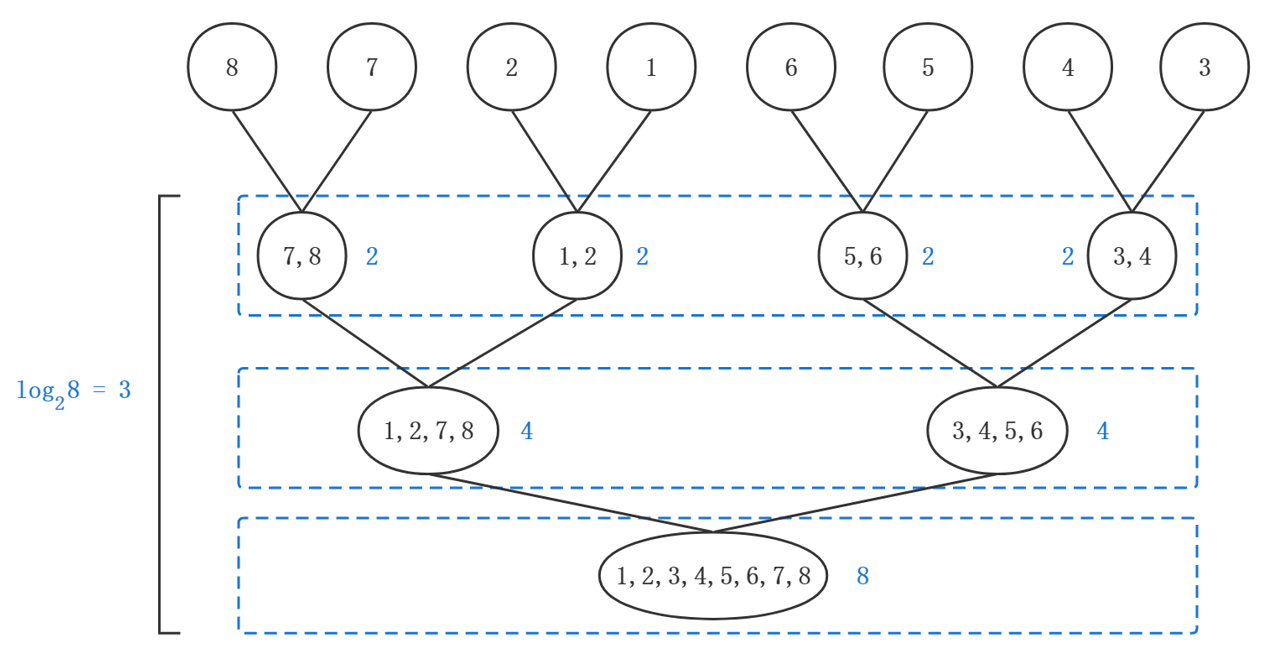
为了进一步说明,我们来改动一下merge函数,将临时数组result作为全局变量。若mergeSort排序的数组长度为n,则临时数组result最大长度将达到n。
var result = []
function mergeSort(arr) {
...
}
function merge(left, right) {
result = []
while (left.length && right.length) {
...
}
if (left.length) {
...
}
if (right.length) {
...
}
return result
}
因此若数组长度为n,占用的最大临时空间则为n,故空间复杂度为O(n)。
# 稳定性
以[3, 3', 2, 1]为例子,将拆分为[3]和[3']两个数组,合并阶段由于3等于3',则临时数组先push推入3,然后继续推入3',排序前后3均位于3'前面,因此归并排序是稳定的。
注意条件
left[0] <= right[0],若条件仅为left[0] < right[0],则会造成排序不稳定
另外归并排序是非原地排序,因为占用了额外空间,也未在原数组上排序。
# 快速排序
快速排序(Quick Sort)也非常形象,即排序性能上非常快,另外快速排序也是分而治之思想的典型例子。核心原理是规定基准值(pivot),然后根据基准值将数组一分为三,包括小于基准值的部分、基准值、大于基准值的部分。
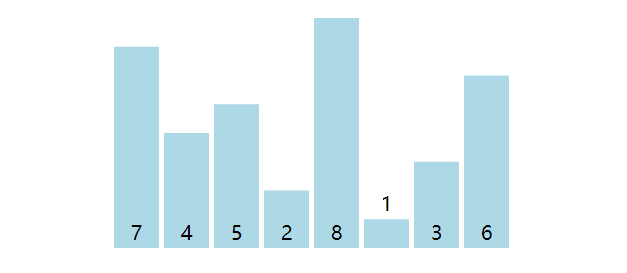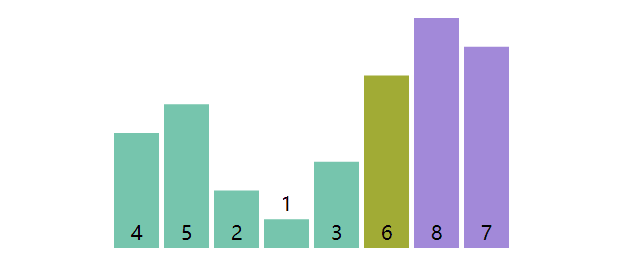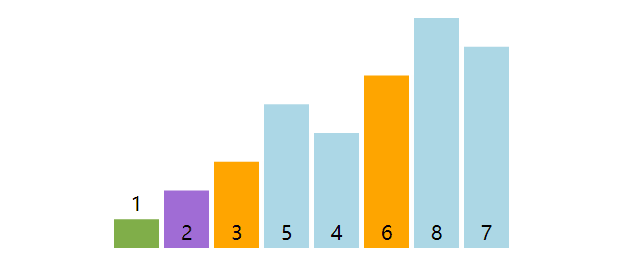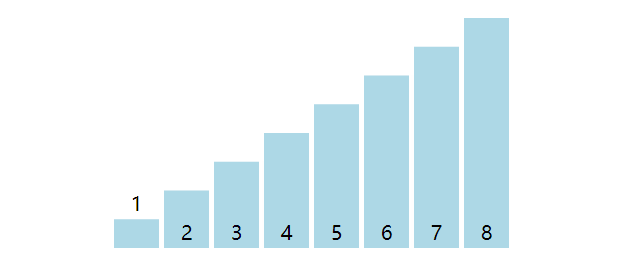
以数组[4, 5, 2, 1, 3]为例来说明分区原理,将数组末尾的元素作为基准值,然后遍历数组,若元素小于或者等于基准值,则将其交换至数组头部。另外注意当遍历到数组末尾处元素时,必然会等于基准值,发生交换,换句话说基准值也会被交换到头部。
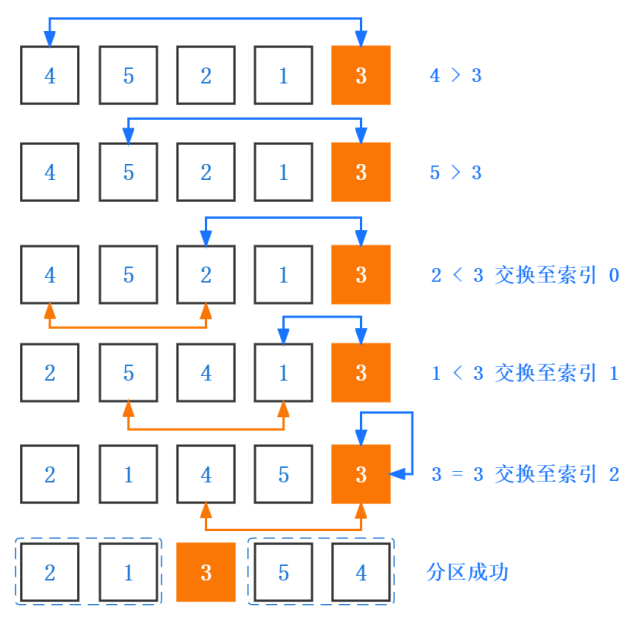
封装为以下函数,其中quickSort对基准值分成的左右部分进行递归排序,partition用于将数组分区。
function quickSort(arr, start = 0, end = arr.length - 1) {
if (start >= end) return
var pivotIndex = partition(arr, start, end)
quickSort(arr, start, pivotIndex - 1)
quickSort(arr, pivotIndex + 1, end)
}
function partition(arr, start, end) {
for (var i = start, j = start, pivot = arr[end]; i <= end; i++) {
if (arr[i] <= pivot) {
swap(arr, i, j++)
}
}
return j - 1
}
数组[7, 4, 5, 2, 8, 1, 3, 6]的排序过程,搭配动图参考效果更加。
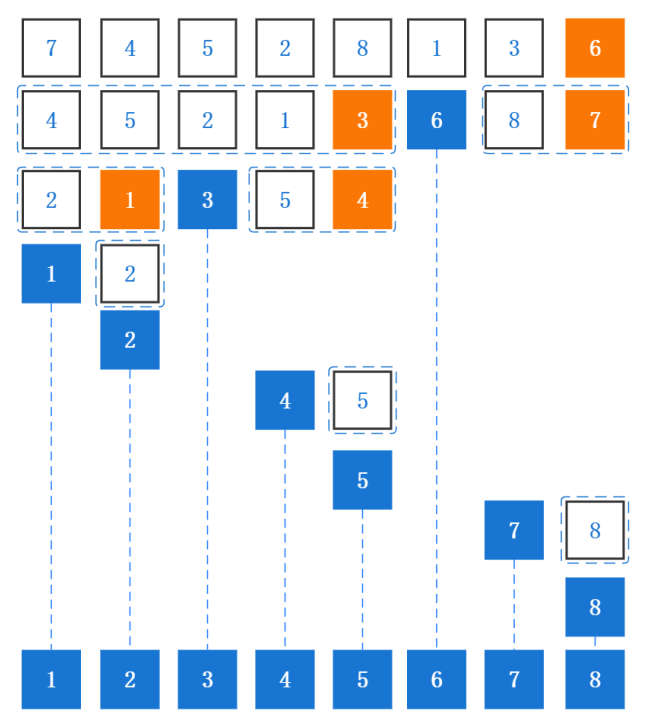
# 特性
# 时间复杂度
最优情况下,每次递归选取的基准值,刚好将数组分为长度相同的两个区间。对规模为n的数组排序,即转换为对两个规模为n / 2的数组排序,符合master主定理条件,时间复杂度为T(n) = 2T(n / 2) + O(n)。容易知道,a = 2,b = 2和d = 1,因此最优情况下的时间复杂度为O(ndlogn) = O(nlogn)。
最坏情况下,数组是升序,例如[1, 2, 3, 4],比较次数为4 + 3 + 2 = 9次。对于长度为n的升序数组,比较次数则为n + (n - 1) + ... + 3 + 2,即(n + 2) * (n - 1) / 2次(算法代码存在差异,比较次数也会有所差异,注意区分),所以最坏情况下的时间复杂度为O(n2)。
快速排序的平均时间复杂度为O(nlogn),对分析过程感兴趣的可以参考文末,此处不作过多说明。
# 空间复杂度
空间复杂度参考两条原则,数组长度和递归深度,其中包括。
- 若为数组,数组长度则为空间复杂度。例如一维数组长度为
n,空间复杂度为O(n)。二维数组长度为n * n,空间复杂度为O(n2),多维以此类推 - 若为递归,递归深度则为空间复杂度的最大值。例如递归深度为
n,空间复杂度为O(n) - 若递归和数组两者都有,则空间复杂度为两者中较大值
快速排序虽然为原地排序,没有占用额外的数组,空间复杂度为O(1)。
但是注意存在递归,最优情况下递归深度为log2n,最差情况下递归深度为n,故快速排序空间复杂度范围为O(logn)到O(n)。
# 稳定性
快速排序是不稳定的,以[3, 1, 3', 2]数组为例子,分区后数组为[1, 2, 3', 3],很明显快速排序是不稳定的。
# 非原地排序版
此版本与归并排序非常类似,但是更加符合快速排序的原理,即数组一分为三个区间。
function quickSort(arr) {
var len = arr.length
if (len < 2) return arr
var pivot = arr[len - 1]
var left = arr.filter((v, i) => v <= pivot && i !== len - 1)
var right = arr.filter(v => v > pivot)
return quickSort(left).concat(pivot, quickSort(right))
}
最优情况下,数组规模n转换为两个n / 2规模的数组,T(n) = 2T(n / 2) + O(n),filter时间复杂度为O(n),多个也是O(n),根据master主定理,时间复杂度为O(nlogn)。
最差情况下,即升序,例如[1, 2, 3, 4],比较次数为4 + 3 + 2。长度为n的数组,比较次数为n + (n - 1) + ... + 3 + 2,即(n + 2) * (n - 1) / 2,时间复杂度为O(n2)。
空间复杂度与归并一致,均为O(n),仅最后一次concat拼接时,占用的空间才会达到最大长度n,之前占用的空间都已经被释放,另外此排序是稳定的。
# 计数排序
计数排序(Count Sort)也非常形象,是非比较排序,原理是开辟一个新数组,然后遍历原数组,将数据值转换为新数组的键,键上的值记录数据值出现的次数。
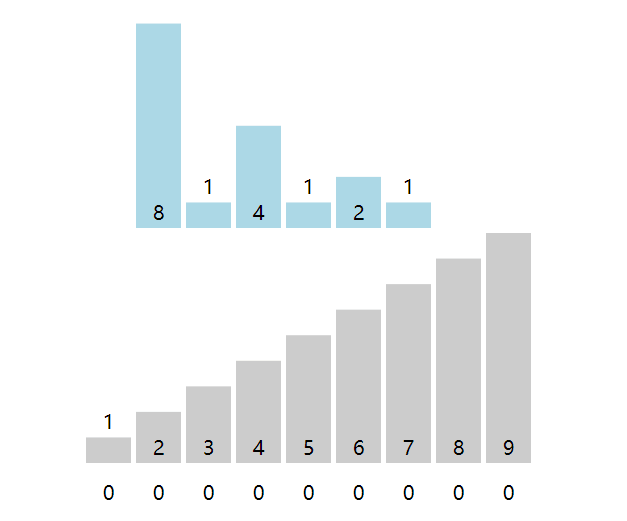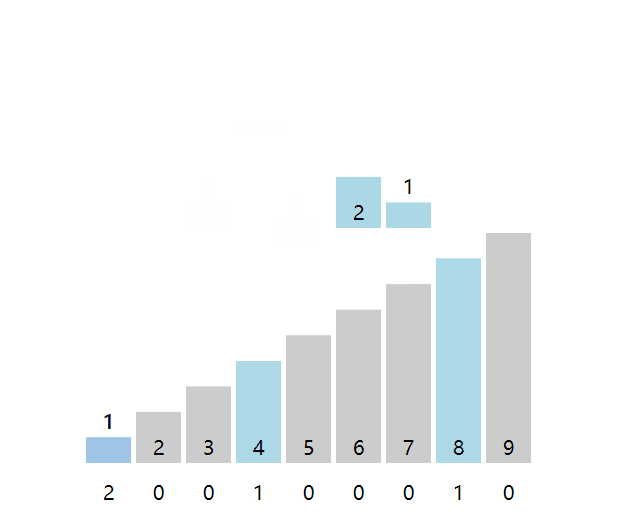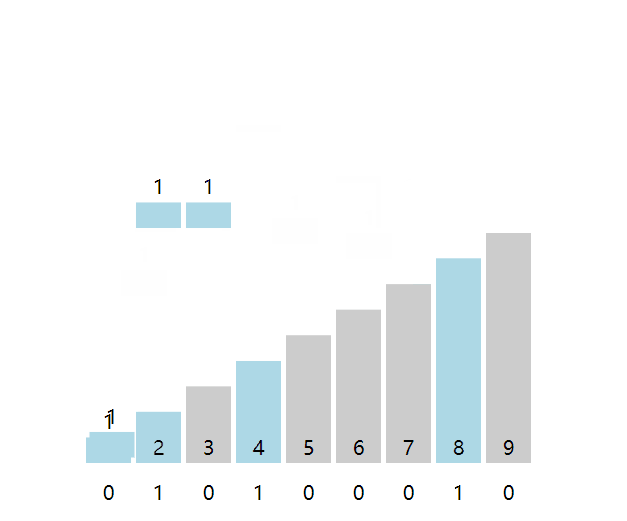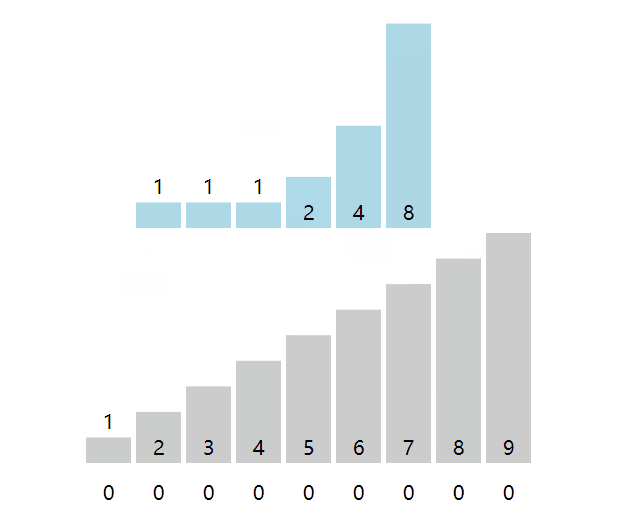
封装为以下函数,注意新数组中可能存在很多的empty空位,for循环不会跳过空位。
;counts为计数数组,例如数组[0, 1, 3, 1],生成的计数数组counts为[1, 2, empty, 1],表示数值0有1个,数值1有两个,数值3有1个。
function countSort(arr) {
var value, counts = [], result = []
for (var i = 0; i < arr.length; i++) {
value = arr[i]
counts[value] = counts[value] || 0
counts[value]++
}
for (var j = 0; j < counts.length; j++) {
while (counts[j] > 0) {
result.push(j)
counts[j]--
}
}
return result
}
以上countSort函数无法排序负数,引入min最小值偏移量。
function countSort(arr) {
var value, counts = [], result = []
const min = Math.min(...arr)
for (var i = 0; i < arr.length; i++) {
value = arr[i] - min
counts[value] = counts[value] || 0
counts[value]++
}
for (var j = 0; j < counts.length; j++) {
while (counts[j] > 0) {
result.push(j + min)
counts[j]--
}
}
return result
}
# 特性
以上计数排序的循环次数为n + n + n + k次,其中获取最小值循环n次,生成计数数组循环n次,while循环恰好为count总数,也就是原数组长度n,k为计数数组长度,故时间复杂度为O(n + k)。
空间复杂度为O(n + k),k为计数数组counts的长度,n为结果数组result的长度。
另外以上计数排序不是原地排序,并且不稳定。
# 稳定版
在计数数组之上,衍生出了累加数组,何为累加数组呢?即累加数组中的元素都是计数数组对应元素与之前元素之和。
比如计数数组[1, 2, 3],生成的累加数组为[1, 3, 6]。累加数组的第三个元素6就是计数数组的第三个元素3与之前元素1和2相加的和。
var counts = [1, 2, 3], adds = []
for (var i = 0; i < counts.length; i++) {
counts[i] = counts[i] || 0
for (var sum = 0, j = i; j > -1; j--) {
sum += counts[j]
}
adds[i] = sum
}
adds // [1, 3, 6]
若累加数组就用counts表示呢?
var counts = [1, 2, 3]
for (var i = 1; i < counts.length; i++) {
counts[i] = counts[i] || 0
counts[i] += counts[i - 1]
}
counts // [1, 3, 6]
数组[2, 1, 2, 0, 2, 1],计数数组为[1, 2, 3],累加数组为[1, 3, 6],排序结果result为[0, 1, 1, 2, 2, 2]。
现在思考下累加数组的作用呢?
以累加数组第一个元素1(索引0)为例,表明了数值0一定位于结果数组result的0(1 - 0)索引处。若有相同数值,例如第二个元素3(索引1),表明数值1最后的位置一定位于result的2(3 - 1)的索引处。
很明显发现,累加数组就是保存了数值在结果数组中的位置信息,相同数值则保存的是最后出现的位置。
封装为以下函数,注意生成result时,是倒序循环的原数组,保证了稳定性。
function countSort(arr) {
var counts = [], result = []
for (var value, i = 0; i < arr.length; i++) {
value = arr[i]
counts[value] = counts[value] || 0
counts[value]++
}
for (var j = 1; j < counts.length; j++) {
counts[j] = counts[j] || 0
counts[j] += counts[j - 1] || 0
}
for (var value, index, k = arr.length - 1; k > -1; k--) {
value = arr[k]
index = counts[value] - 1
result[index] = arr[k]
counts[value]--
}
return result
}
数组[0, 1, 3, 1]的排序过程,其中累加数组为[1, 3, 3, 4]。
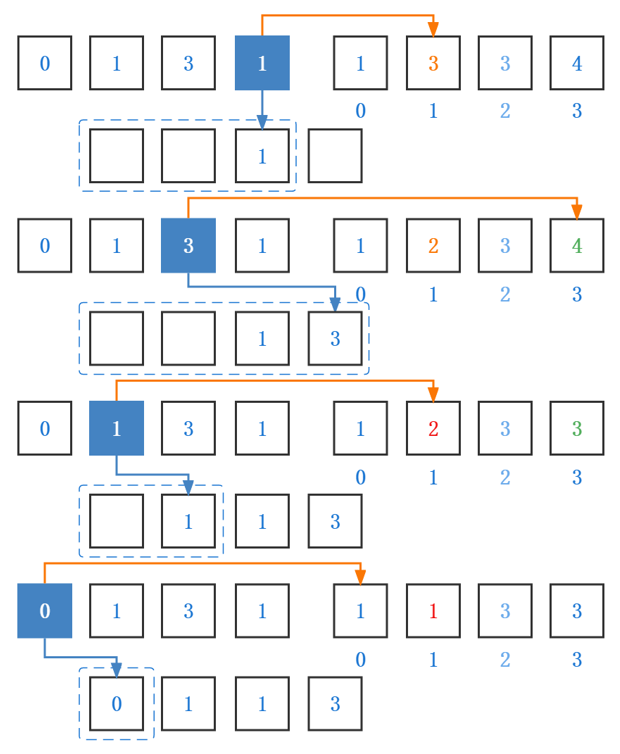
引入min偏移量可排序负数。
function countSort(arr) {
var counts = [], result = []
const min = Math.min(...arr)
for (var value, i = 0; i < arr.length; i++) {
value = arr[i] - min
counts[value] = counts[value] || 0
counts[value]++
}
for (var j = 1; j < counts.length; j++) {
counts[j] = counts[j] || 0
counts[j] += counts[j - 1] || 0
}
for (var value, index, k = arr.length - 1; k > -1; k--) {
value = arr[k] - min
index = counts[value] - 1
result[index] = arr[k]
counts[value]--
}
return result
}
稳定版计数排序的循环次数为n + n + k + n,因此时间复杂度为O(n + k),空间复杂度为O(n + k),非原地排序。
计数排序的缺点也很明显。
- 无法排序非整数,局限性很高
- 适用于数据范围较小的数组,数据范围较大时耗费内存
- 数据量大的时候可能存在排序效率不如比较排序的情况
# 基数排序
基数排序(Radix Sort)也非常形象,运用了桶的概念,桶的数量由基数决定的。例如十进制数的基数为10,则桶的数量为10个,保存位数在0 ~ 9之间的数。
数组中的最值决定排序次数,每次排序获取数值的位数,放入对应的桶中,然后循环桶将数值取出。由于桶是有序的,取出的数在位数上则也是有序的,并且排序是由低位开始,故排序结束数组将是有序的。

以数组[1, 61, 865, 65, 5]为例子,最大值为865,则排序3轮,分别为个位十位百位。
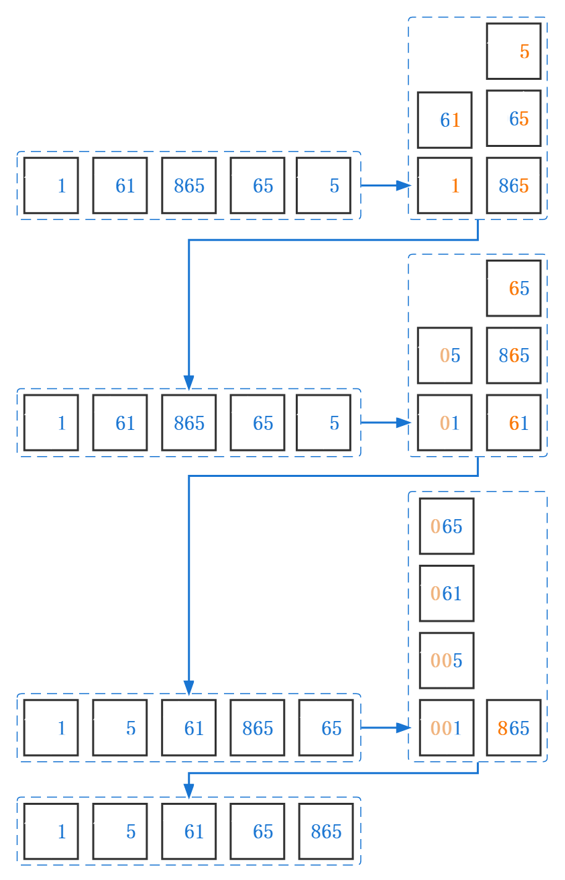
封装为以下函数。
function radixSort(arr) {
var n = 1, buckets = [], len = arr.length, max = Math.max(...arr)
do {
for (var i = 0; i < len; i++) {
const value = arr[i]
const digit = Math.floor(value / n) % 10
buckets[digit] = buckets[digit] || []
buckets[digit].unshift(value)
}
for (var j = 0, k = 0; j < 10; j++) {
buckets[j] = buckets[j] || []
while (buckets[j].length) {
arr[k] = buckets[j].pop()
k++
}
}
n *= 10
} while ((max = Math.floor(max / 10)))
}
其中digit表示取出数字的固定位,以865为例。
// 个位
Math.floor(865 / 1) % 10 // 5
// 十位
Math.floor(865 / 10) % 10 // 6
// 百位
Math.floor(865 / 100) % 10 // 8
# 特性
以上基数排序的循环次数为n + k * 2n,其中获取最大值循环n次,do ... while循环k次,k由最大值决定。2n为n + n,do ... while循环体中,数字放入桶中循环n次,从桶中取出循环n次(while总的循环次数恰好为原数组长度n),故时间复杂度为o(kn)。
空间复杂度为O(n + k),其中n为原数组长度,k为桶的数量或者基数。
由于占用了额外的空间,基数排序为非原地排序,但是为稳定排序。
# 负数版
以上基数排序的排序范围非常小,只能排序0和正数,引入偏移量可排序负数。
function radixSort(arr) {
var buckets = [], len = arr.length, n = 1, min = Infinity, max = -Infinity
for (var i = 0; i < len; i++) {
if (arr[i] > max) max = arr[i]
if (arr[i] < min) min = arr[i]
}
max -= min
do {
for (var i = 0; i < len; i++) {
const value = arr[i] - min
const digit = Math.floor(value / n) % 10
buckets[digit] = buckets[digit] || []
buckets[digit].unshift(value)
}
for (var j = 0, k = 0; j < 10; j++) {
buckets[j] = buckets[j] || []
while (buckets[j].length) {
arr[k] = buckets[j].pop() + min
k++
}
}
n *= 10
} while ((max = Math.floor(max / 10)))
}
负数版的时间空间复杂度与之前的基数排序一致,注意负数版由于存在数值与min加减运算的情况,是不稳定的。
例如数组[1, 3, new Number(1)],之前版本将排序为[1, Number, 3],而负数版则为[1, 1, 3],排序的元素由new Number(1)变成了1,去探讨稳定性没有多大意义。你也可以理解为扩大了排序范围,但是丢失了稳定性,毕竟元素都改变了。
# 桶排序
桶排序(Bucket Sort / Bin Sort)即将待排序元素放入对应的桶,桶间有序,桶内无序,然后局部排序桶内元素即可。其中计数排序和基数排序就属于一类比较特殊的桶排序。
严格来说,桶排序不是一种排序方式,因为独立的桶内部还是依赖于常见的排序,更多的是一种数组预处理的过程,或者说是一种优化方式,符合分而治之的思想,对于处理大批量的数据将会非常有用。
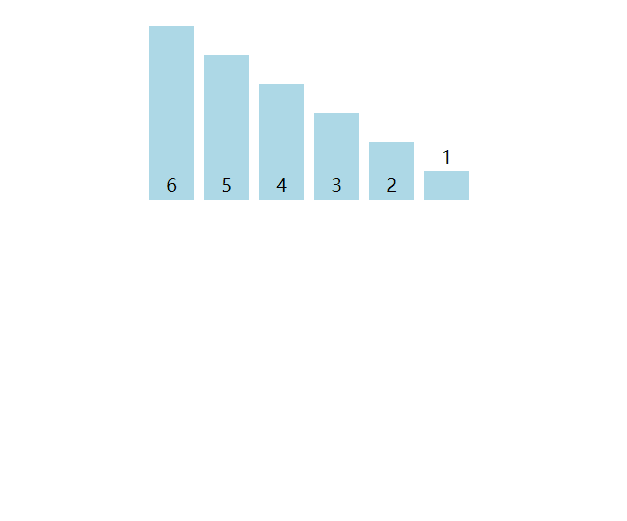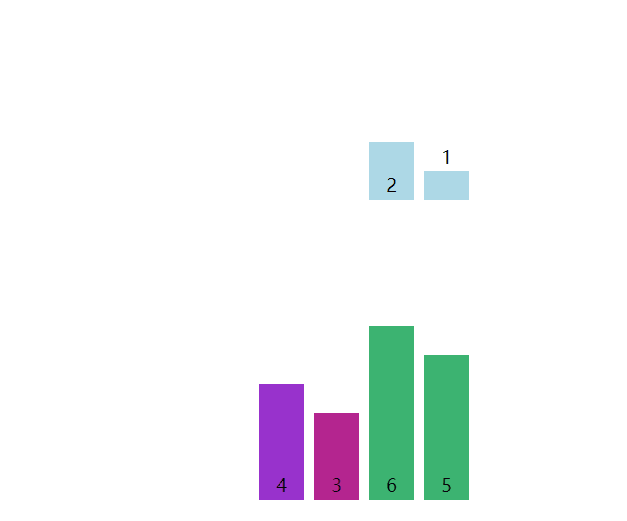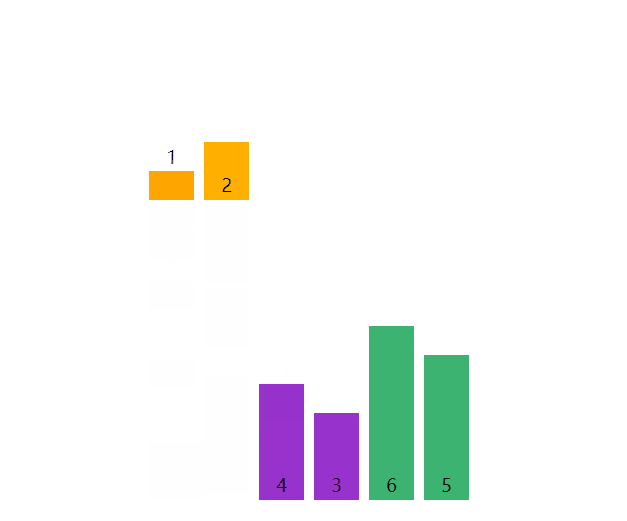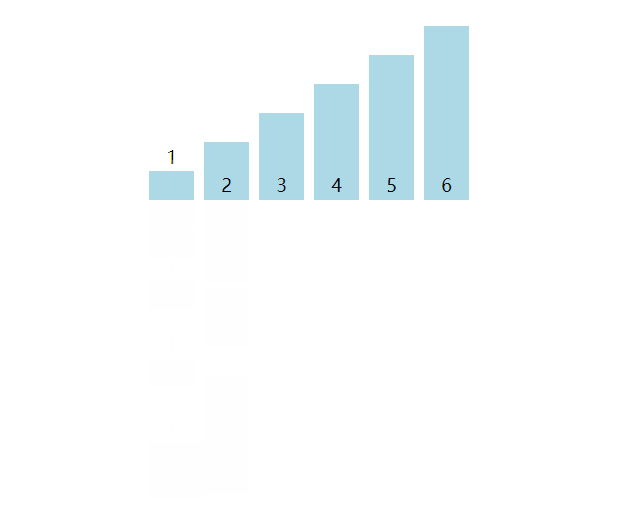
封装为以下函数,其中桶的数量为count,由最值和桶内的数据个数size决定。合理的size将决定桶内数据的排序方式,插入排序在数据量不大的时候就比较合适。当size为1时,桶排序与计数排序将高度相似。
function bucketSort(arr, size = 6) {
var buckets = [], count = 0, n = 0, len = arr.length, min = Infinity, max = -Infinity
for (var i = 0; i < len; i++) {
if (arr[i] > max) max = arr[i]
if (arr[i] < min) min = arr[i]
}
count = Math.floor((max - min) / size) + 1
for (var i = 0; i < count; i++) {
buckets[i] = []
}
for (var i = 0; i < len; i++) {
var index = Math.floor((arr[i] - min) / size)
buckets[index].push(arr[i])
}
for (var i = 0; i < buckets.length; i++) {
var item = buckets[i]
insertionSort(item)
for (var j = 0; j < item.length; j++) {
arr[n] = item[j]
n++
}
}
}
以数据量为100000的数组为例,桶排序与插入排序的效率对比。
var first = [], second = []
for (var i = 0; i < 100000; i++) {
var value = (Math.random() > 0.5 ? 1 : -1) * Math.floor(100000 * Math.random())
first.push(value)
second.push(value)
}
...
console.time('bucketSort')
bucketSort(first)
console.timeEnd('bucketSort')
console.time('insertionSort')
insertionSort(second)
console.timeEnd('insertionSort')
// bucketSort: 11.285888671875 ms
// insertionSort: 1559.23193359375 ms
# 特性
# 时间复杂度
桶排序的时间复杂度分为三个部分,包括。
- 获取最值,根据最值和桶内元素的个数创建桶,元素分配到桶中
- 所有的桶独立排序
- 桶元素依次取出,完成排序
第一步为O(n + k + n),其中获取最值循环n次,创建桶循环k次,k为桶的个数,元素分配到桶中循环n次。第三步循环k个桶,将n个元素取出,即O(n + k)。
第二步选择的排序方式不同,时间复杂度也会不同。例如插入排序,时间复杂度为O(n)到O(n2)之间,k个规模为m(n / k)的数组时间复杂度为O(km)到O(km2)之间,代入m = n / k则为O(n)到O(n2 / k)范围。
合并的时间复杂度为O(n + k)到O(n2)。
# 空间复杂度
空间复杂度,桶排序的稳定性都由内部的排序决定。例如内部为插入排序,则桶排序的空间复杂度为O(n + k),n为桶内数组的长度之和,也就是原数组的长度,k为桶的数量。插入排序为稳定排序,因此以上桶排序也是稳定的。
另外由于占用了额外空间,桶排序则不是原地排序。
桶排序的缺点也很明显。
- 占用空间,桶的数量越多,空间复杂度就越高,相对的时间复杂度就越低。当桶的数量与数组个数相等时,将退化成计数排序
- 数据要相当紧凑,太分散会创建很多空的桶
# 堆排序
堆排序(Heap Sort)也非常形象,主要原理是运用堆的性质,依次取出数组中的最大值。
# 大顶堆
堆排序中提到的堆是一种叫做完全二叉树的数据结构,包括大顶堆和小顶堆。
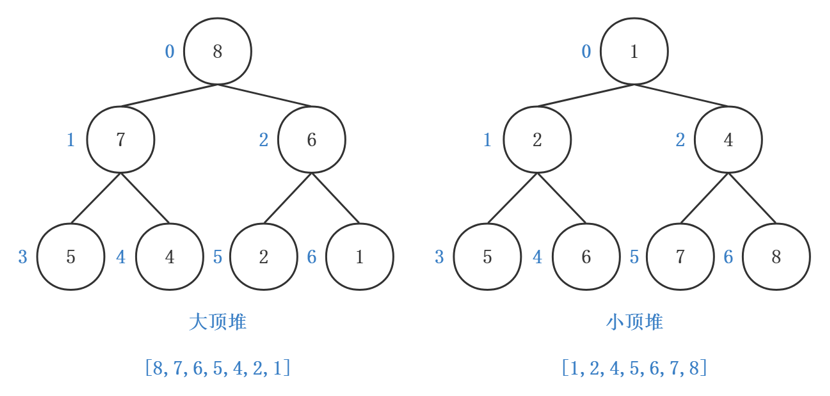
以大顶堆为例,它的根节点一定是最大值,且每个节点都大于或者等于左右子节点的值。
若当前节点的索引为i,则左子节点为i * 2 + 1,右子节点为i * 2 + 2,父节点为Math.floor((i - 1) / 2)。
注意观察,最后一个叶子节点的父节点,一定是最后一个非叶子节点。最后一个非叶子节点之前的节点,也全部都是非叶子节点。
数组长度为n,最后一个叶子节点为n - 1。n - 1代入Math.floor((i - 1) / 2)则有Math.floor((n - 1 - 1) / 2),化简即最后一个非叶子节点为Math.floor(n / 2) - 1。
# 堆化
那么如何将一个无序序列构建成大顶堆呢?
根据大顶堆的性质,非叶子节点均大于等于左右子节点。因此先要找到所有的非叶子节点,然后交换当前节点和左右子节点,形成父节点大于子节点的结构。
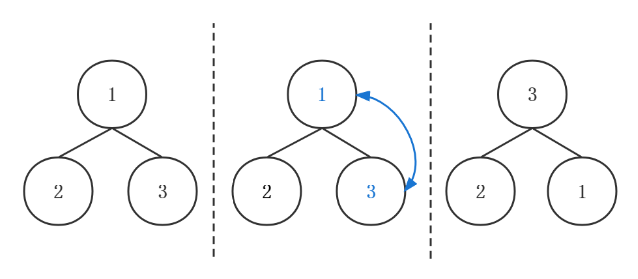
又如何找到所有的非叶子节点呢?
刚才已经知道,最后一个非叶子节点之前的所有节点都是非叶子节点,且最后一个非叶子节点的索引为Math.floor(n / 2) - 1,故索引在0到Math.floor(n / 2) - 1之间都是非叶子节点。
以数组[6, 5, 1, 7, 8, 4]为例,Math.floor(6 / 2) - 1 = 2,故索引为0 1 2的节点都是非叶子节点。
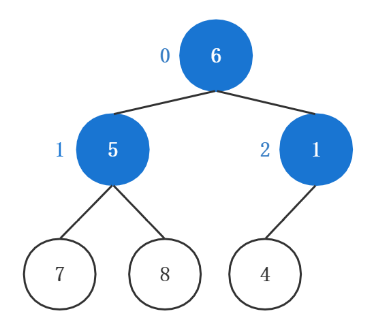
思考一个问题,是自顶向下从0开始循环到2,还是自底向上从2开始循环到0呢?
假设当前节点位于二叉树第i层,如果是自顶向下,在与第i + 1层的子节点发生交换后,第i层并不能保证小于第i - 1层,还要向上回溯第i - 1层。
如果是自底向上,在与第i + 1层交换后,事实上也不能保证第i层小于第i - 1层。但是注意,由于是自底向上,循环了第i层后,紧接着会继续循环i - 1层,而此时就保证了第i层小于第i - 1层。
还是以数组[6, 5, 1, 7, 8, 4]为例,两种情况的过程为。
// 自顶向下
6 6 8 8 8
/ \ / \ / \ / \ / \
5 1 --> 8 1 --> 6 1 --> 7 1 --> 7 4
/ \ / / \ / / \ / / \ / / \ /
7 8 4 7 5 4 7 5 4 6 5 4 6 5 1
// 自底向上
6 6 6 8 8
/ \ / \ / \ / \ / \
5 1 --> 5 4 --> 8 4 --> 6 4 --> 7 4
/ \ / / \ / / \ / / \ / / \ /
7 8 4 7 8 1 7 5 1 7 5 1 6 5 1
自底向上的动态过程。

构建大顶堆过程封装为buildMaxHeap函数。
function buildMaxHeap(arr) {
for (var i = Math.floor(arr.length / 2) - 1; i > -1; i--) {
heapify(arr, i)
}
}
function heapify(arr, i) {
var n = arr.length,
max = i,
left = i * 2 + 1,
right = i * 2 + 2
if (left < n && arr[left] > arr[max]) {
max = left
}
if (right < n && arr[right] > arr[max]) {
max = right
}
if (max !== i) {
swap(arr, i, max)
heapify(arr, max, n)
}
}
var arr = [6, 5, 1, 7, 8, 4]
buildMaxHeap(arr)
console.log(arr) // [8, 7, 4, 6, 5, 1]
# 排序
构建出大顶堆,排序过程就非常简单了。
大顶堆的根节点为最大值,将根节点与末尾节点交换,取出最大值,然后对剩下的节点持续构建成大顶堆。
注意取出最大值后,二叉树除了根节点不符合当前节点大于等于子节点的性质之外,剩下的所有节点都符合。因此仅仅对根节点执行堆化即可。
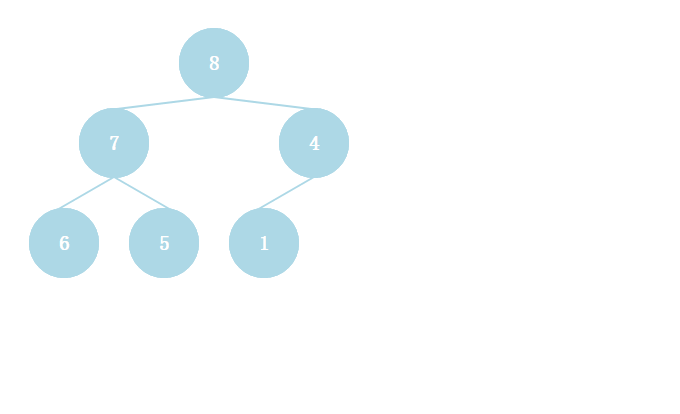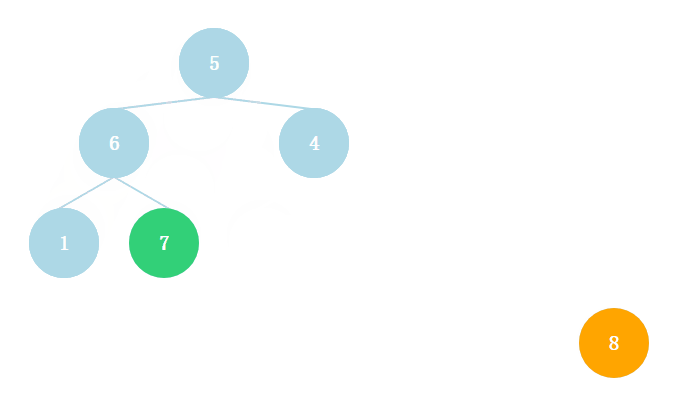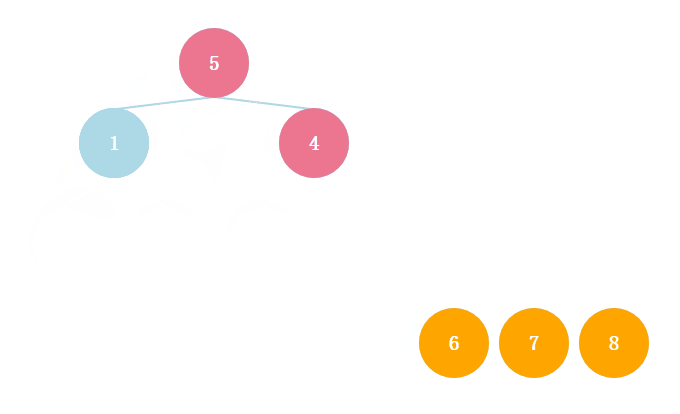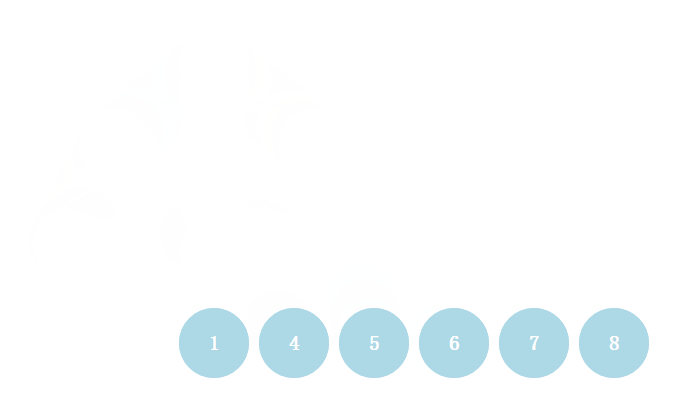
封装为以下函数。
function heapSort(arr) {
var len = arr.length
buildMaxHeap(arr, len)
for (var j = len - 1; j > 0; j--) {
swap(arr, 0, j)
heapify(arr, 0, j)
}
}
function buildMaxHeap(arr, len) {
for (var i = Math.floor(len / 2) - 1; i > -1; i--) {
heapify(arr, i)
}
}
function heapify(arr, i, n = arr.length) {
var max = i,
left = i * 2 + 1,
right = i * 2 + 2
if (left < n && arr[left] > arr[max]) {
max = left
}
if (right < n && arr[right] > arr[max]) {
max = right
}
if (max !== i) {
swap(arr, i, max)
heapify(arr, max, n)
}
}
# 特性
堆排序的时间复杂度为O(nlogn),空间复杂度为O(1),没有占用额外的空间,即也是原地排序。
以数组[2, 1, 2']为例子,排序后为[1, 2', 2],因此堆排序是不稳定的。
# 参考
- 排序可视化 (opens new window)
- 快速排序的时间复杂度分析 (opens new window)
- 阮一峰快速排序 (opens new window)
- 如何看待文章《面试官:阮一峰版的快速排序完全是错的》? (opens new window)
# 🎉 写在最后
🍻伙伴们,如果你已经看到了这里,觉得这篇文章有帮助到你的话不妨点赞👍或 Star (opens new window) ✨支持一下哦!
手动码字,如有错误,欢迎在评论区指正💬~
你的支持就是我更新的最大动力💪~
GitHub (opens new window) / Gitee (opens new window)、GitHub Pages (opens new window)、掘金 (opens new window)、CSDN (opens new window) 同步更新,欢迎关注😉~
