# 关于取消 ES6 函数尾递归的相关探究
# 前言
;ES6中的尾递归优化非常实用,于是乎去初步探究。但是你会非常失望,发现绝大多数浏览器已经不支持,node也在很早的版本中取消了支持。关于尾递归优化的相关文档,也都仅仅是简单提及,只言片语,优化点原理几乎就不提,了解起来非常麻烦。
因此查阅了很多文档,并简单汇总,希望可以由斐波那契数列,逐步展开,引导你了解尾递归的知识点。
以下内容中的知识点包括。
STC、TCO和STC分别是什么- 尾调用优化的优化点是什么
V8为何取消支持尾调用优化PTC与STC的优缺点
# 尾调用
# 调用栈
;JavaScript调用栈用于存储代码执行期间的所有上下文,每一个执行上下文也叫调用帧,栈内活动通常为。
- 运行全局代码,创建全局执行上下文并压入栈中
- 函数被调用时,创建函数执行上下文并压入栈顶。函数执行完成后,对应的上下文弹出
- 全局代码执行结束,全局执行上下文弹出,调用栈清空
function bar(x) {
return x // A
}
function foo(x) {
return bar(x) + 2 // B
}
foo(1) // C
以上代码调用栈的活动情况如下。
bar context
├── x
└── Line B
foo context foo context foo context
├── x ├── x ├── x
└── Line C └── Line C └── Line C
global context --> global context --> global context --> global context --> global context
├── bar ├── bar ├── bar ├── bar ├── bar
└── foo └── foo └── foo └── foo └── foo
函数在执行前, 除了初始化变量对象、作用域链和this之外,调用帧上还将保存函数返回位置的地址信息。例如bar函数执行完成后,返回代码行B,在bar函数的调用帧就保存了代码行B的位置地址。
# 尾调用优化
将代码改造为尾调用,即在函数的最后一步只调用函数。
function bar(x, y) {
return x + y // A
}
function foo(x) {
return bar(x, 2) // B
}
foo(1) // C
现在来思考一个问题,函数foo运行完最后一行代码后,将执行权交接给了bar函数,foo剩下的唯一用处就是将返回值传递给代码行C。
如果我们将bar函数的返回位置直接修改为C,不再通过B,那么foo是不就没用了啊。
因此我们就可以将foo的调用帧删除了,但是注意要在foo运行后,交出执行权给bar之前删除,因为foo函数中可能有其它的代码要执行。
再来看看调用栈的活动情况。
bar context
foo context ├── x
├── x ├── y
└── Line C └── Line C
global context --> global context --> global context --> global context
├── bar ├── bar ├── bar ├── bar
└── foo └── foo └── foo └── foo
以上则是我们经常说的尾调用优化(TCO,Tail Call Optimization),与规范中提到的PTO(Proper Tail Calls)是同一个东西,只是叫法不同。
尾调用优化的优点也很明显,当函数关系复杂时,调用栈的长度会大大减小,从而节省内存,避免出现堆栈溢出的情况。缺点则是,为了改造为尾调用,部分函数的参数将调整,函数的语义将不同于原本的语义,出现偏差,造成维护成本增加。另外此优化是浏览器层面的,依赖引擎支持,会出现兼容性差异。
# 斐波那契
普通形式的斐波那契数列。
// 1 1 2 3 5 8 13 21 34 55
function f(n) {
if (n <= 2) {
return 1
}
return f(n - 1) + f(n - 2)
}
# 最大栈长度
执行f(4)时的调用栈活动。
f(1) f(0)
f(2) f(2) f(2) f(2) f(2) f(1) f(1) f(0)
f(3) f(3) f(3) f(3) f(3) f(3) f(3) f(3) f(3) f(2) f(2) f(2) f(2) f(2)
f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4) --> f(4)
更加直观的节点图。
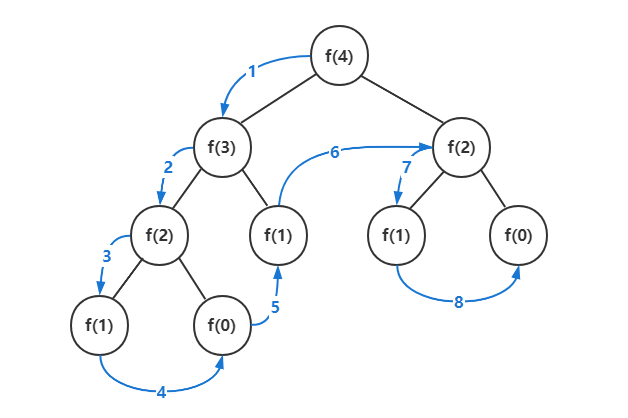
可以归纳出f(n)执行期间的最大调用栈长度为n。
# 节点数
斐波那契的通项公式a(n)为。
节点数量g(n)为。
;JavaScript代码也贴一下,你可以测试验证。
function a(n) {
const sqrt5 = Math.sqrt(5)
return (Math.pow(((1 + sqrt5) / 2), n) - Math.pow(((1 - sqrt5) / 2), n)) / sqrt5
}
function g(n) {
return 2 * a(n + 1) - 1
}
# 浏览器
以下代码可用于测试浏览器的调用栈长度。
function getDeep() {
try {
return 1 + getDeep()
} catch (err) {
return 1
}
}
getDeep()
相关浏览器的调用栈长度为。
Chrome:11419Firefox:25607Opera:22862Edge:3718IE11:1982
然后看另外一种情况。
function getDeep() {
try {
new Array(10000).fill(new Array(100).fill(0))
return 1 + getDeep()
} catch (err) {
return 1
}
}
getDeep()
;Chrome浏览器下打印8973,因此可以发现,除了浏览器和浏览器版本的不同,会影响执行栈长度之外,函数体的大小和函数内变量的数量也会影响栈的长度。
# 常见误区
;f(40)运行耗时大概800ms左右,另外根据刚才的结论,f(40)的最大栈长度为40,节点数为331160281。
console.time('f(40)')
console.log(f(40)) // 102334155
console.timeEnd('f(40)') // f(40): 800.323974609375 ms
然后运行f(100)试试,容易知道最大栈长度为100,节点数g(100)约为1.146295688027638e+21。
注意节点数为约数,原因在于
JavaScript中数值的有效位数为16位,运算过程中可能存在舍入,造成精度丢失
实际你会发现,浏览器将无响应,且长时间处于加载状态。
我们用f(40)来粗略地估计f(100)的执行时长,假设每个节点运行耗时相同,注意实际每个节点耗时肯定不一样,但是足够说明问题了。
var cost = 800 / 331160281 // 单个节点耗时
var millisecond = 12 * 30 * 24 * 60 * 60 * 1000 // 一年的毫秒数
// f(100) 耗时(年)
1.146295688027638e+21 * cost / millisecond // 89029
粗略估计f(100)将运行约89029年(无参考性),因此浏览器无响应的根本原因是,节点数过于庞大,浏览器长时间处在运算中。
注意不是爆栈,不是爆栈,f(100)的最大栈长度仅为100,远远小于浏览器的调用栈长度(Chrome调用栈长度11419)。除非是执行f(11419),才会存在爆栈的情况,另外受函数体的大小和变量数量的影响,实际根本不用达到11419就会爆栈。
由于一些官方文档排版错误,很容易被误导是爆栈导致浏览器无响应,注意区分
# 尾递归
节点数过多造成运行超时,现在来考虑优化。
尝试将斐波那契修改为尾递归形式,尾递归即函数尾调用自身。
function f(n, m = 1, o = 1) {
if (n <= 2) {
return o
}
return f(n - 1, o, m + o)
}
;f(4)的调用栈活动。
f(2, 2, 3)
f(3, 1, 2) f(3, 1, 2) f(3, 1, 2)
f(4, 1, 1) --> f(4, 1, 1) --> f(4, 1, 1) --> f(4, 1, 1) --> f(4, 1, 1)
更加直观的节点图。
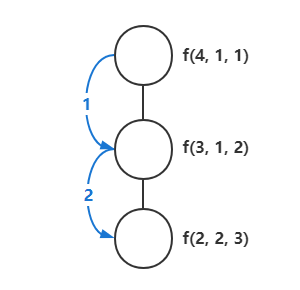
可归纳出f(n)执行期间的最大调用栈长度和节点数均为n - 1。
;f(100)的节点数仅99,浏览器运行非常流畅。
console.time('f(100)')
console.log(f(100)) // 354224848179262000000
console.timeEnd('f(100)') // f(100): 0.107177734375 ms
甚至可以运算f(6000),Infinity说明f(6000)的数值已经非常大了。
console.time('f(6000)')
console.log(f(6000)) // Infinity
console.timeEnd('f(6000)') // f(6000): 1.869873046875 ms
斐波那契的普通方式运行f(100)浏览器长时间无响应,而递归方式可以轻松运行f(6000),对代码的执行效率提升可以说是爆炸级的。
应当明确的是,尾递归方式仅仅优化了节点数,即减少了函数的调用次数,以此避免程序超时,但是代码还是会存在堆栈溢出爆栈的情况的,例如f(10000)。
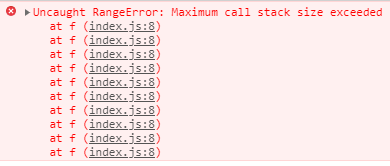
# 尾递归优化
文初提及的尾调用优化(PTC),可用来减少调用栈,避免堆栈溢出,实际就是用来解决爆栈问题的,另外递归函数中的PTC又被称为尾递归优化。
目前PTC仅在Safari浏览器和部分node版本中支持,node中仅6.0.0 ~ 8.6.0版本支持,5.12.0及之前的版本不支持,从8.7.0开始不再提供支持。
查看当前node版本选项,包含--harmony_tailcalls即表示支持PTC。
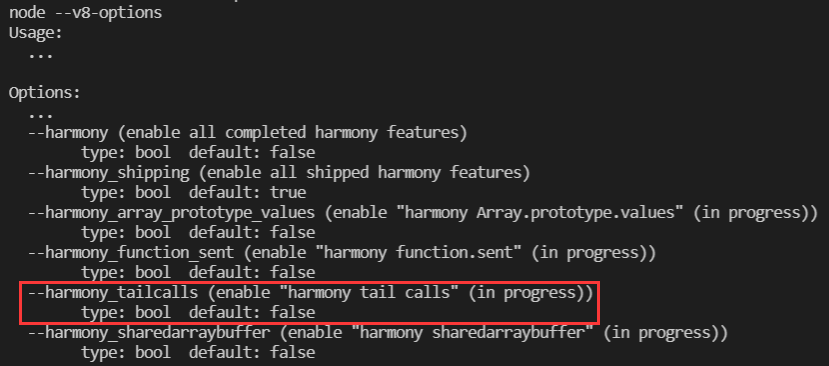
我们在node的8.6.0版本中运行斐波那契(尾递归形式)f(100000)。
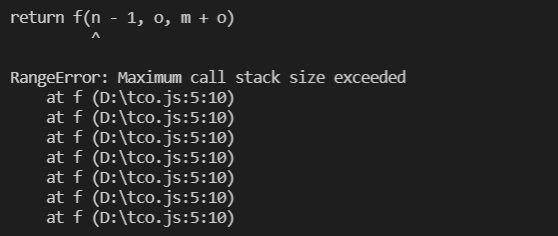
;node的调用栈长度为8961,必然会爆栈。
尝试开启PTC优化。
node --use-strict --harmony-tailcalls tco.js
--use-strict表示开启严格模式,--harmony-tailcalls或者--harmony选项都能开启PTC
;f(100000)成功运行,理论上f(n)参数多大都能运行,但是注意节点数会影响运行时间。
console.time('f(100000)')
console.log(f(100000)) // Infinity
console.timeEnd('f(100000)') // f(100000): 13.768ms
为什么仅严格模式PTC才会生效呢?
我们在非严格模式运行以下代码,注意baz不是尾调用。
function bar(x, y, z) {
console.log(bar.caller === foo) // true
console.log(bar.arguments.callee.caller === foo) // true
return x + y + z // A
}
function foo(x, y) {
return bar(x, y, 3) // B
}
function baz(x) {
foo(x, 2) // C
}
baz(1) // D
;bar.caller将返回调用bar的那个函数foo,bar.arguments.callee将返回bar函数。
那么引擎是如何获取的呢?
对于bar.caller,在调用栈中引擎将根据当前栈帧(bar栈帧),查找到它的上一个栈帧foo,然后返回那个栈帧所对应的函数,即foo函数。
bar context
├── x
├── y
├── z
└── Line B
foo context
├── x
├── y
└── Line C
baz context
├── x
└── Line D
global context
├── bar
├── foo
└── baz
假设PTC在非严格模式下支持,优化后foo栈帧将被删除,bar返回的代码行被修改为C。那么bar.caller和bar.arguments.callee.caller都将返回baz。
bar context
├── x
├── y
├── z
└── Line C
baz context
├── x
└── Line D
global context
├── bar
├── foo
└── baz
能够发现优化后,造成bar.caller和bar.arguments.callee.caller都失真了,显然不是我们想看到的,为了保证结果正确,如果禁用func.caller和func.arguments问题将迎刃而解。
而恰好,严格模式就禁用了它们,但是注意禁用不单单是因为PTC,还有其他原因。
# 主要原因
既然尾递归优化如此好用,那么为何绝大多数浏览器都不支持呢?
# 隐式优化
有两个主要原因,第一个原因就是隐式优化的问题,看了很多关于此问题的文章,讲的都是含糊不清,模棱两可。
现在来换一个角度,我来问你来答。
你如何确定写出了正确的尾递归?
你可能会说,我来一行一行检查代码,保证递归函数确实为尾部调用。
如果浏览器支持PTC,你将如何确定你的尾递归是被PTC优化了呢?
你可能会说,可以找一个没有开启PTC的浏览器,互相对比运行时间。
现在,你有没有发现,相较于你的日常开发,以上工作完全就是在浪费时间。另外为了写出正确的尾递归,你还要不断修改代码,不断调试。
如果你的尾递归正确,并且你也成功验证了浏览器的PTC优化。
function f() {
...
return f()
}
f()
以上代码在你的网页里时,当你打开浏览器,浏览器将无响应,且长时间处在加载状态。紧接着你将打开控制台,但是你会发现,控制台并没有任何报错,因为死循环被PTC优化了,将很难抛出爆栈错误。
那么你能否确定是资源加载慢的问题,还是别的代码有问题,还是死循环的问题等?以上代码可能还相对容易,但是代码体量大了之后,几乎很难排查出来。
最后一个问题,倘若浏览器不支持PTC,排查出原因最快多久呢?
哈哈,抢答,分分钟的事,浏览器抛出爆栈,很快就能定位。
因此概况来讲,也就是隐式优化的过程是不受开发者控制和了解的。
# 栈帧丢失
第二个原因,由于PTC会删除中间帧,造成堆栈不连续,开发者在断点调试时,将难以理解执行情况。例如堆栈为A B C D E F(栈顶F),优化后为A F,你会非常纳闷,怎么就从函数A执行到函数F了呢。
其次,栈帧丢失也会影响error.stack的错误原因收集,进而造成客户端错误收集和分析工具失效。
function bar() {
throw new Error()
}
function foo() {
return bar()
}
function baz() {
foo()
}
baz()
以上代码未PTC优化的error.stack堆栈。
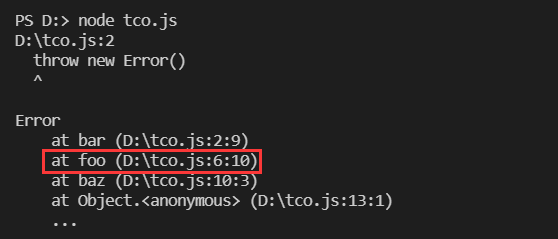
;PTC优化(v8.6.0)的error.stack堆栈,对比发现,foo栈帧已被删除。
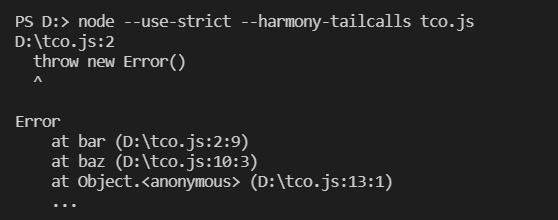
为了解决以上error.stack异常堆栈缺失的问题,又衍生了另外一种机制,即用 shadow stack (opens new window)(影子堆栈)来恢复被删除的中间帧,为了区别,恢复的调用帧将被置为灰色。
在Safari浏览器已经实现了影子堆栈,但是,V8和DevTools团队认为,控制台的堆栈应当始终与真实情况一致,保证控制台是绝对可靠的。另外,由于是将删除的栈帧又恢复,对浏览器性能也会造成很大影响。
# STC
由于以上原因,V8强烈支持用特殊语法的方式来表示PTC,称为语法尾调用(STC,Syntactic Tail Calls)。
比较好看且直观的一种语法。
// 普通函数
function f() {
return continue f()
}
// 箭头函数
const f = () => continue f()
为什么更加推荐STC呢?
开发者可以确认是否写出了正确的尾递归,例如return continue 1 + f()的非尾递归将在编译阶段就抛出错误。另外对于尾递归死循环无响应的情况,可以通过增删关键字continue进一步确认。
因此可以说STC让隐式优化的过程可控了。但是栈帧丢失的问题,还是没有办法根本解决,毫无进展也是必然了(已被遗弃 (opens new window))。
# 优化
既然浏览器层面暂时无法实现,那就来手动优化,原理也很简单,即减少调用栈长度,防止溢出爆栈。
尾递归的斐波那契。
function f(n, m = 1, o = 1) {
if (n <= 2) {
return o
}
return f(n - 1, o, m + o)
}
# 循环
调用栈中仅包括f(n)一帧。
function f(n, m = 1, o = 1) {
while (n > 2 && n--) {
[m, o] = [o, m + o]
}
return o
}
f(40) // 102334155
f(100000) // Infinity
缺点也很明显,递归不容易改写为循环,另外循环在语义上也不太容易理解。
# 蹦床函数
蹦床函数trampoline内部为循环结构。
function trampoline(f) {
while (f && typeof f === 'function') {
f = f()
}
return f
}
function f(n, m = 1, o = 1) {
if (n <= 2) {
return o
}
return f.bind(null, n - 1, o, m + o)
}
trampoline(f(40)) // 102334155
trampoline(f(100000)) // Infinity
;f(40)调用栈活动。
f.bind(, 39)() f.bind(, 38)() f.bind(, 37)()
f(40) --> ___ --> trampoline() --> trampoline() --> trampoline() --> trampoline() --> trampoline() --> trampoline() --> trampoline() ...
原理上并不是函数内继续调用函数,而是返回一个新的函数,避开了递归执行。同时不会在原函数的调用帧上创建新的调用帧,而是原函数的调用帧弹出后,新的函数帧才会入栈,堆栈将始终在一帧或两帧之间弹跳。视觉上类似弹跳蹦床,蹦床函数名称也由此而来。
___ ___ ___
___ ___ ___
蹦床函数也存在一些缺点。
比如原递归函数要做改动,将返回值修改成返回新的函数。运行f(n)时,要嵌套执行trampoline(f(n)),不容易理解。性能上相对于原递归函数,也将会有所下降。
还有一个严重缺点,即只适用于返回结果为非函数的尾递归。
倘若递归结果就是返回一个函数。
function f(n) {
if (n <= 1) {
return g
}
return f(n - 1)
}
function g() {
return 1
}
f(4) // ƒ g()
引入蹦床函数。
function f(n) {
if (n <= 1) {
return g
}
return f.bind(null, n - 1)
}
function g() {
return 1
}
trampoline(f(4)) // 1
结果不一致了,原因很简单,返回的结果由于是函数,被蹦床函数执行了。
# 闭包
闭包形式的优化。
function tco(func) {
var value
var active = false
const accumulated = []
return function accumulator(...args) {
accumulated.push(args)
if (!active) {
active = true
while (accumulated.length) {
value = func.apply(this, accumulated.shift())
}
active = false
return value
}
}
}
const f = tco(function fibonacci(n, m = 1, o = 1) {
if (n <= 2) {
return o
}
return f(n - 1, o, m + o)
})
f(40) // 102334155
f(100000) // Infinity
;tco为优化函数,返回accumulator函数。fibonacci为原始的尾递归函数,f为tco优化后的函数。
;tco闭包保存了四个私有变量,包括value、active和accumulated以及参数func。
以下为f(40)调用栈活动,注意f(n)运行之前,fibonacci等价于func,f等价于accumulator。
f(39) f(38) f(37)
func(40) func(40) func(40) func(39) func(39) func(39) func(38) func(38) func(38)
tco() --> ___ f(40) --> f(40) --> f(40) --> f(40) --> f(40) --> f(40) --> f(40) --> f(40) --> f(40) --> f(40) --> f(40) --> f(40) --> f(40) ...
堆栈可视化,保持在一帧到三帧之间活动。
___ ___ ___
___ ___ ___ ___ ___ ___
___ ___ ___ ___
优点为原函数不用改动,语义清晰,容易迭代。缺点也很明显,调用栈活动时间长,造成性能大幅下降。
# 小结
- 尾调用即函数尾部调用函数,若调用自身则为尾递归
- 函数改写为尾递归,可减少函数的调用次数,避免程序超时,不能解决爆栈的问题
PTC或TCO,即尾调用优化,用以消除尾调用的中间帧,防止爆栈。- 递归函数的
PTC,即为尾递归优化 PTC,存在隐式优化和栈帧丢失两个主要原因。隐式优化的过程很难受开发者的控制,栈帧丢失不利于调试和错误收集- 影子堆栈可解决栈帧丢失的问题,但是非常耗费性能
STC,用特殊语法来表示PTC,可解决隐式优化的问题,但是依然不能解决栈帧丢失- 尾递归的手动优化,包括改写为循环、蹦床函数、闭包,各有优缺点
# 参考
- 哪些表达式为尾调用 (opens new window)
- PTC 兼容性 (opens new window)
- PTC 根本原因 (opens new window)
- STC (opens new window)
- STC / PTC 知乎讨论 (opens new window)
# 🎉 写在最后
🍻伙伴们,如果你已经看到了这里,觉得这篇文章有帮助到你的话不妨点赞👍或 Star (opens new window) ✨支持一下哦!
手动码字,如有错误,欢迎在评论区指正💬~
你的支持就是我更新的最大动力💪~
GitHub (opens new window) / Gitee (opens new window)、GitHub Pages (opens new window)、掘金 (opens new window)、CSDN (opens new window) 同步更新,欢迎关注😉~
